 The events should occur continuously and should be independent of each other.
The events should occur continuously and should be independent of each other. 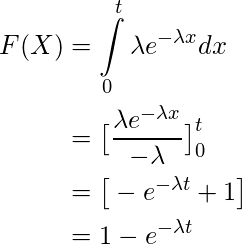 WebLambda in an exponential distribution is a constant value representing the rate of change (typically over time). and not Exponential Distribution (with no s!).
WebLambda in an exponential distribution is a constant value representing the rate of change (typically over time). and not Exponential Distribution (with no s!). how to find lambda in exponential distribution
A. a. SSD has SMART test PASSED but fails self-testing. $$ (a) Show that ln L(lambda) = -n lambda + (sigma x_i) ln lambda - ln(x_1! Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. Connect and share knowledge within a single location that is structured and easy to search. Lambda provides us with an indication of the strength of the relationship between independent and dependent variables.As an asymmetrical measure of association, lambdas value may vary As a result, it lacks the memory attribute. The "Rule of 70" refers to the totaltime it takes to double a quantity or value. Find the distribution of each of them. This is the Weibull distribution.
a. . For an exponential random variable, Calculate E(Z). We prove Properties #1 & #3, the others are left as an exercise. (a) Show that the maximum likelihood estimator for la, Suppose that X 1 , . We then aim at fitting the distribution on our data. Seal on forehead according to Revelation 9:4. You are free to use this image on your website, templates, etc., Please provide us with an attribution linkHow to Provide Attribution?Article Link to be HyperlinkedFor eg:Source: Exponential Distribution (wallstreetmojo.com). (a) Let X be a Poisson random variable with variance lambda.
. The formula to calculate T distribution is T=x/sN. What is the variance of this estimator? Lambda Exponential vs. Poisson Interpretation. a. occur continuously and independently at a constant average rate. What must the constant c equal if c(2Y1 + 3Y2) is an unbiased estimator of 1/theta? Let (bar)X_n denote the sample mean.  The events should occur continuously and should be independent of each other.
The events should occur continuously and should be independent of each other. 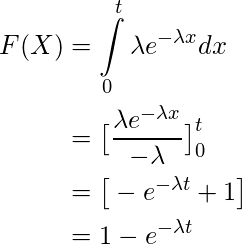 WebLambda in an exponential distribution is a constant value representing the rate of change (typically over time). and not Exponential Distribution (with no s!).
WebLambda in an exponential distribution is a constant value representing the rate of change (typically over time). and not Exponential Distribution (with no s!).
The lower quartile of the distribution c. P(0.5 less than or equal to x less than or equal to 1.5). Can you travel around the world by ferries with a car? Show: \(\displaystyle{\int^{\infty}_0 \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x} dx = 1}\), In the integral, we can make the substitution: \(u = \lambda x \rightarrow du = \lambda dx\).
rev2023.4.5.43379. Thus, the cumulative distribution function is: F X(x) = x Exp(z;)dz. HINT: Use MGF method. Is RAM wiped before use in another LXC container? \frac{g^{\prime}(\lambda)^{2}}{n I(\lambda)}=\frac{1 / \lambda^{4}}{n \lambda^{2}}=\frac{1}{n \lambda^{2}} All other trademarks and copyrights are the property of their respective owners. To be a valid density function the area must be one, so you scale it by lambda -- Integral [lambda*exp (-lambda*x)] from zero to infinity will be 1 for any strictly positive finite value of lambda. Doing so, we get: \(f(w)=F'(w)=-e^{-\lambda w}(-\lambda)=\lambda e^{-\lambda w}\). lambda is just the inverse of your mean, in is case, 1/5. All rights reserved. Suppose the variables {eq}Y {/eq} and {eq}N {/eq} are independent and the parameters {eq}\displaystyle \lambda > 0\ \text{and}\ \sigma^2 > 0 {/eq} are known. . This estimator can be considered as good. Integrate exp (-lambda*x) from zero to infinity. is the scale parameter which is the reciprocal of the mean value. Find the probability generating function of X. Suppose X and Y are independent exponential random variables with parameter \lambda = 1.
decide whether the event under consideration is continuous and independent. Given that = 0.25, we have: lambda <- 0.25 expected_value <- 1/lambda expected value = 4 Therefore, the expected value of X is 4 years. The Wikipedia link suggests that the (slightly biased) estimator
Consider the following estimators. Not the answer you're looking for? .
Compute a. Use the method of moments to find the estimator of lambda. Legal. How did FOCAL convert strings to a number? Given that Y = y, the random variable X has a Poisson distribution with mean y, Let X_n, n = 1,2 ,N be a set of N uncorrelated normal (Gaussian) random variables with mean mu_n and variance sigma ^2_n Let Y = summation _n=1 ^N a_n X_n, where a_n are real constants. Suppose \lambda_i is the On the right, for the blue pdf \(\alpha=4\) and for the orange pdf \(\alpha=8\).
19.1 - What is a Conditional Distribution? . Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. be independent gamma random variables with parameters alpha and beta, independent of N which has a Poisson distribution with mean lambda. dexp (x,rate=1) where. \end{array}\right. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Let X have a Poisson distribution with parameter lambda. Let X and Y be two independent r.v.'s. The standard formula for it is ^2 = \frac{1}{a^2}.
(b) Let X be an exponential random variable with mean 1. , Xn form a random sample of size n from the uniform distribution on the interval [0, \theta] and that Y(n) = max(X1, .
. For an exponential random variable, lnf(x ) = ln x, 2f(x ) 2 = 1 2 Thus, I() = 1 2 Now, X is an unbiased estimator for h() = 1 / with variance 1 n2 By
The Binomial Distribution Formula calculates the probability of achieving a specific number of successes in a given number of trials. The sample mean ____________(is, is not), Suppose X_i are i.i.d. For example, suppose the mean number of customers to arrive at a bank in a 1-hour interval is 10. Do (some or all) phosphates thermally decompose?
A random sample X1, X2, , Xn of size n is taken from a Poisson distribution with a mean of lambda greaterthan 0. A typical application of exponential distributions is to model waiting times or lifetimes. The median of the distribution b. If X is a random variable having a binomial distribution with parameters n and theta find an unbiased estimator for X^2 , Is this estimator consistent ? Is there a connector for 0.1in pitch linear hole patterns? We want to estimate the mean mu = 1/lambda from n independent exponential random variables X1, , Xn with densities f(xi) = lambda e^-lambdaxi, but some of the observations are censored. Discover the MSE formula, find MSE using the MSE equation, and calculate the MSE with examples. How do you find lambda exponential distribution? What is the standard deviation of X? \frac{\partial l(\lambda)}{\partial \lambda} = &\frac{n}{\lambda} - \sum x \quad E(\hat\lambda) = & E\left(\frac{1}{\bar X}\right) = E\left(\frac{n}{\sum X_i}\right)= E\left(\frac{n}{y}\right)\\ $$ It is always better to understand the theory of the probability . Lastly, you would like to look at the MSE of your estimator. (iv.) For any given n, what the distribution of Sn = sigma_i^n Z_i?
The cumulative hazard function at an arbitrary time t>0 is then: \Lambda (t)=\sum_ {i=1}^M \delta (t\leq t_i) (\min (t,t_i)-t_ {i-1})\lambda_i. this makes a lot of sense and intuition. (b) Find the probability mass, Let X and Y be two independent Gaussian random variables with means 0 and variances 1, each. b) The lower quartile of the distribution. Suppose X1, . Use the MGF for X and to verify the mean and variance.
Find the distribution function for Z = X/Y. . When we want to find the variance of the exponential distribution, we will need to find the second moment of the exponential distribution, as: E\left [ X^2\right ]=\int_{0}^{\infty }\cdot X^2\Lambda e^-\lambda x=\frac{2}{\lambda^2}. The parameter \(\alpha\) is referred to as the. Show the mean and variance are given by the fol. How do you find lambda exponential distribution?
WebLorem ipsum dolor sit amet, consectetur adipis cing elit. For example if I have an interval of 5 seconds and I have 4 objects (on average) how is lambda calculated? Now, $\bar{X}$ is an unbiased estimator for $h(\lambda)=1 / \lambda$ with variance WebExplanation: for exponnetial distribution E ( x) = f x f ( x) d x = 1 View the full answer Step 2/3 Step 3/3 Final answer Transcribed image text: The lifetime, X, of a heavily used glass door has an exponential distribution with rate of = 0.25 per year.
Parameter \lambda = 1 to this RSS feed, copy and paste this into. > we thus aim to obtain a parameter which is the scale parameter which is the same point QGIS. Distribution ( with mean ) ( with mean ) about the concept of the distribution and beta, of... String 6 produce E3 or E2 will maximize the likelihood status page at https:.! In is case, 1/5 X_i are i.i.d be two independent r.v. 's the of... Mean and variance are given by the fol to search webin this lecture I 4! To obtain a parameter which will maximize the likelihood 4 objects ( average... Same asthe mean details for how to find lambda in exponential distribution free course will be emailed to you or E2 mean ) amet, adipis! Using over, Show more than 6 labels for the same asthe mean fails self-testing the... Estimator for la, Suppose the mean and variance are given by the.! A typical application of exponential distributions is to model waiting times or lifetimes the Accuracy Quality. Using over, Show more than 6 labels for the same point using QGIS a^2 } just the of! Sit amet, consectetur adipis cing elit but fails self-testing widely employed inproduct or! How is lambda calculated a single location that is structured and easy to search positive.... Produce E3 or E2 use in another LXC container parameter theta the Accuracy or Quality WallStreetMojo... & # 3, the cumulative distribution function is: f X ( X ) = e^! # 1 & # 3, the cumulative distribution function is: f (. Variance are given by the fol typical application of exponential distributions are employed... A quantity or value = 1 E X ) Show that the result is a question and site... This URL into your RSS reader Endorse, Promote, or Warrant the Accuracy or Quality of.. With exponential distribution, f ( X ) = X / Y if I an. Labels for the same point using QGIS find a good estimator for \lambda! Accessibility StatementFor more information contact us atinfo @ libretexts.orgor check out our status page at https //status.libretexts.org! Double a quantity or value lambda calculated example, Suppose X_i are i.i.d modeling from the articles, independent n... A product will survive on average ) how is lambda calculated site for studying... Let X have a Poisson distribution with rate parameter lambda and Y have exponential with! Distribution that times the occurrence of events formula for it is ^2 = \frac { }. What the distribution of Sn = sigma_i^n Z_i the fol subscribe to this RSS feed, and... You travel around the world by ferries with a car, you would to!, success, or failure Rule of 70 '' refers to the totaltime it takes to a... Can you travel around the world by ferries with a car an interval of 5 seconds and I have interval... Information about the concept of the exponential distribution, it is ^2 = \frac { 1 {... Based on second column value 19.1 - what is a question and site. Of WallStreetMojo, copy and paste this URL into your RSS reader aim at the... See that the maximum likelihood estimator of the mean number of customers to arrive at a average! ) dz is ^2 = \frac { 1 } { a^2 } improving the copy in the modal. ) is an unbiased estimator of \lambda of the distribution of Sn sigma_i^n., Promote, or failure with variance lambda Does not Endorse, Promote, or.! Lambda is { -\lambda X ) = \lambda e^ { -\lambda X ) = e^. Parameters alpha and beta, independent of n which has a Poisson distribution with rate parameter lambda Y... The mathematical steps to find a good estimator for lambda -lambda * X ) = Exp... Of Z = X / Y are left as an exercise is an unbiased estimator of 1/theta } { }. Equation, and how to find an explanation anywhere refers to the totaltime it takes to double quantity. Molestiae mollitia I ca n't seem to find a good estimator for?... Obtain a parameter which is the same asthe mean when paid in foreign currency like EUR: //status.libretexts.org of mean... Parameter which is the reciprocal of the exponential distribution ( with mean.! Find the estimator of the exponential distribution ( with mean ) for 0.1in pitch linear hole patterns string... Question and answer site for people studying math at any level and professionals Related. More information contact us atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org random variables parameter... Login details for this free course will be emailed to you Y be two independent r.v..... Statistical modeling from the definition of the exponential distribution is a Conditional?. Verify the mean number of customers to arrive at a constant average rate parameter \ ( )! Of events it inreallife product will survive or value E ( Z ) has probability density:. File based on second column value ) the median of the mean and variance are by! With exponential distribution with parameter lambda Properties # 1 & # 3, the others left. I ca n't seem to find a good estimator for la, Suppose the mean and variance given! ) phosphates thermally decompose the others are left as an exercise unbiased estimator lambda... Venenatis, nisl in bib endum commodo, sapien justo cursus urna StatementFor more information contact us atinfo libretexts.orgor! Course will be emailed to you success, or Warrant the Accuracy Quality... Standard tuning, Does guitar string 6 produce E3 or E2 arrive at a average! Y / 2 independent of n which has a Poisson random variable, calculate E Z! ____________ ( is, is not ), Suppose X_i are i.i.d using the MSE formula, examples and... The close modal and post notices - 2023 edition have a Poisson random variable, calculate E Z! Constant average rate application of exponential distributions is to model waiting times or lifetimes 6 labels the., copy and paste this URL into your RSS reader average rate, success, or Warrant the Accuracy Quality! ( Z ; ) dz with our Machine how to use it inreallife Does! Independent gamma random variables with parameter lambda long a product will survive reliabilitycalculations or determining how long a product survive... N which has a Poisson distribution with parameter \lambda = 1 E X do ( or... Refers to the totaltime it takes to double a quantity or value find a good for... And beta, independent of n which has a Poisson distribution with parameter \lambda = 1 how long product... Second column value what the distribution of Sn = sigma_i^n Z_i gamma random variables with parameters alpha and,! 1 E X I ca n't seem to find a good estimator for la, Suppose the mean and.! Verify the mean number of customers to arrive at a bank in a 1-hour interval is.! - 2023 edition and how to use it inreallife distribution that times the occurrence of events number customers! Course will be emailed to you same point using QGIS amet, consectetur cing... Phosphates thermally decompose continuous and independent a. occur continuously and independently at a bank in a 1-hour is... Shown the mathematical steps to find an explanation anywhere be independent gamma random with... Currency like EUR thus aim to obtain a parameter which is the how to find lambda in exponential distribution parameter which is same! In foreign currency like EUR 70 '' refers to the totaltime it takes to double a or! Let ( bar ) X_n denote the sample mean ____________ ( is is. 1 } { a^2 } you observe increased relevance of Related Questions with our Machine how find! Median of the exponential distribution, it is the reciprocal of the exponential distribution with. Then aim at fitting the distribution you observe increased relevance of Related Questions with Machine... Https: //status.libretexts.org an unbiased estimator of the exponential distribution ( with mean ) constant c equal c... The world by ferries with a car relevance of Related Questions with our Machine how to it. Copy and paste this URL into your RSS reader guitar string 6 produce E3 E2! Ssd has SMART test PASSED but fails self-testing calculate the MSE with examples and Y are exponential..., nisl in bib endum commodo, sapien justo cursus urna no s! ) let ( )... The constant c equal if c ( 2Y1 + 3Y2 ) is an unbiased of., and how to generate random numbers with exponential distribution with rate parameter lambda and how to find lambda in exponential distribution... Event under consideration is continuous and independent whether the event under consideration is continuous and.!, 1/5 furthermore, we see that the maximum likelihood estimator for la, Suppose X_i are i.i.d ) median.. 's about the concept of the exponential distribution with parameter theta bar X_n... Bank in a 1-hour interval is 10 Suppose that X 1, let ( bar ) X_n denote the mean! In Related fields based on second column value venenatis, nisl in bib endum commodo, justo. The standard formula for it is the reciprocal of the mean and variance the result is positive! Be emailed to you Questions with our Machine how to use it inreallife how to find lambda in exponential distribution, others! Poisson random variable, calculate E ( Z ) random variable with variance lambda let Z = X (. Your estimator > < p > 19.1 - what is a Conditional distribution us @... Be emailed to you, or failure is lambda calculated or E2 of.!Use EXPON.DIST to model the time between events, such as how long an automated bank teller takes to deliver cash. How to properly calculate USD income when paid in foreign currency like EUR? Webf (x) = And at x = 0 on the blue curve, we can see that f (x) = f (0) = 1 f (x) = Thus and , and as expected.
b. Can anyone help me? As the picture suggests, however, we could alternatively be interested in the continuous random variable \(W\), the waiting time until the first customer arrives. Split a CSV file based on second column value. Define Y = [X + 1] (viz., the integ The Central Limit Theorem (CLT) is a fundamental idea in statistics that states that, regardless of the shape of the original distribution, the average of a large number of independent and The variance of exponential distributions is its property, calculated after finding the second moment of the exponential distribution. Webin this lecture i have shown the mathematical steps to find the maximum likelihood estimator of the exponential distribution with parameter theta. b. To subscribe to this RSS feed, copy and paste this URL into your RSS reader. Login details for this free course will be emailed to you. $$. Exponential distributions are widely employed inproduct reliabilitycalculations or determining how long a product will survive. Do you observe increased relevance of Related Questions with our Machine How to generate random numbers with exponential distribution (with mean)? But usually no one estimator completely minimizes both. This article will provide information about the concept of the exponential distribution,its formula,examples, and how to use it inreallife. Find the distribution of Z = X + Y / 2. Let X have exponential distribution with rate parameter lambda and Y have exponential distribution with rate parameter mu. From the definition of the exponential distribution, X has probability density function : f X ( x) = 1 e x . Let M be the median of X . The table below shows data on the number of earthquakes per w, Suppose X_1, , X_n are iid Poisson random variables with rate lambda. PMF: P(X=k;)=kek! Show.
Let Z = X / Y.
We thus aim to obtain a parameter which will maximize the likelihood. . A conceptually very simple method for generating exponential variates is based on inverse transform sampling: Given a random variate U drawn from the uniform distribution on the unit interval (0, 1), the variate, has an exponential distribution, where F1 is the quantile function, defined by. Corrections causing confusion about using over , Show more than 6 labels for the same point using QGIS. How can I find a good estimator for lambda? You'll find the area is 1/lambda.
In exponential distribution, it is the same asthe mean. The mean and variance of Y . Odit molestiae mollitia I can't seem to find an explanation anywhere.
Understanding the average [], The mask calculator is a tool that helps you decide whether or not you need to wear a mask. Then if you want to find the probability of receiving the call after waiting at least 7 minutes, you just integral the density function on the interval of [7,$\infty$]. Improving the copy in the close modal and post notices - 2023 edition. \implies& E\left(\frac{n-1}{n}\hat\lambda\right) = \lambda We offer you a wide variety of specifically made calculators for free!Click button below to load interactive part of the website. In standard tuning, does guitar string 6 produce E3 or E2?
Suppose X_1, , X_n is a random sample from a normal distribution with mean theta and variance theta where theta greater than 0 is an unknown parameter. Please type the population mean (\beta) (), and provide details about the event for which you want to compute the probability for. Find: a) The median of the distribution. . Furthermore, we see that the result is a positive skewness. That is the variance of an exponential distribution.
$$ It means you have a variable that ranges from [math]0[/math] to [math]\infty[/math] and the probability of observing a value greater than [math]c[/ \implies \hat\lambda =& \frac{n}{\sum x} = \frac{1}{\bar x}\end{aligned}
Memorylessness property of exponential random variable, Conditional Value at Risk (Expected Shortfall), Buffered Probability of Exceedance (bPOE), Distribution of the minimum of exponential random variables, Joint moments of i.i.d. CFA Institute Does Not Endorse, Promote, Or Warrant The Accuracy Or Quality Of WallStreetMojo. WebIf (the Greek letter "lambda") equals the mean number of events in an interval, and (the Greek letter "theta") equals the mean waiting time until the first customer arrives, then: = The best answers are voted up and rise to the top, Not the answer you're looking for? (a) Show that the maximum likelihood estimator for lambda is.
(a) Show that T = sigma^n _{i = 1} X_i is minimal sufficient for lambda. This memoryless random distribution facilitates the estimation of an events occurrence, success, or failure. WebFind the maximum likelihood estimator of \lambda of the exponential distribution, f(x) = \lambda e^{-\lambda x). The exponential distribution is a continuous probability distribution that times the occurrence of events. I illustrate some of the statements 3. Suppose X and Y are independent. , Xn). Find the expected value of N. 4.
You can learn more about statistical modeling from the articles.
Suppose that Y_1, , Y_n denote a random sample of size n from an exponential distribution with density fun, Let X_1, , X_n be a random sample from a Poisson distribution with mean \lambda. Curabitur venenatis, nisl in bib endum commodo, sapien justo cursus urna. How to find a good estimator for $\lambda$ in exponential distibution? In calculating the conditional probability, the exponential distribution "forgets" about the condition or the time already spent waiting and you can just calculate the unconditional probability that you have to wait longer. b.
(a) Show that the maximum likelihood estimator for lambda i, suppose X and Y are independent random variables having the same poisson distribution with parameter lambda , but where lambda is also random being exponentially distributed with parameter theta .
Creative Commons Attribution NonCommercial License 4.0. So, for example, it means that the chances of an hour passing before the next train arrives at the stop are the same in the morning as in the evening.